Sludge characteristics: rheological

1. Sludge rheology
Sludge rheology relates to how it flows. This is in turn characterised by its viscosity, which is defined as the relationship between the shear stress and the shear rate.
The shear rate is the rate at which layers of fluid move relative to a surface and to one another. It is the velocity per unit distance (i.e. velocity gradient) where the distance is measured orthogonally (i.e. at right angles) to the direction of the velocity.
The shear stress is the force that arises from applying the shear associated with the shear rate, divided by the area over which the shear applies. It therefore takes units of force per unit area, i.e. the same units as pressure – though it’s not the same parameter as pressure.
The ratio of the shear rate to sheer stress is the viscosity. For a Newtonian fluid, like water, it is constant: there is no change in viscosity with applied shear, and there is therefore a linear relationship between shear stress and shear rate (see below). Other fluid types display non-Newtonian behaviours.
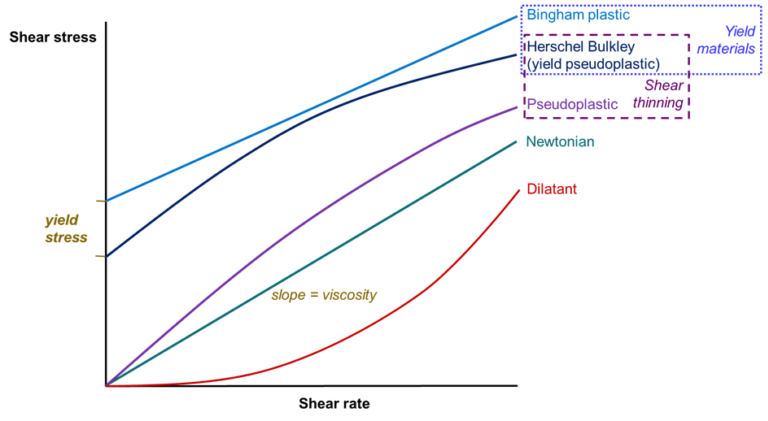
Sludge generally displays Herschel Bulkley behaviour. It has positive shear stress value (called its yield stress) at zero shear rate, and the rate of change of shear stress with shear rate then declines with shear – a characteristic defined as shear-thinning.
The yield stress value means that at very low shear rates the sludge apparent viscosity – the ratio of the shear stress to the shear rate – is extremely high. The viscosity then decreases with increasing shear. This means that the viscosity of the sludge in a practical situation will depend on the flow rate and/or other system parameters defining shear.
2. Sludge viscosity vs other bulk properties
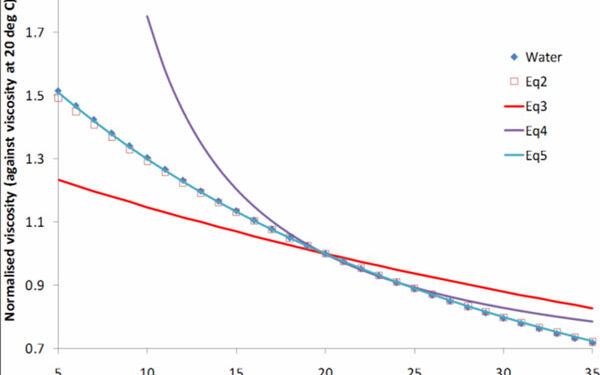
Sludge viscosity can change with both temperature, as with any other fluid, and with solids concentration. A number of different mathematical expressions have been suggested for sludge viscosity vs solids concentration. Many of these take the general form:
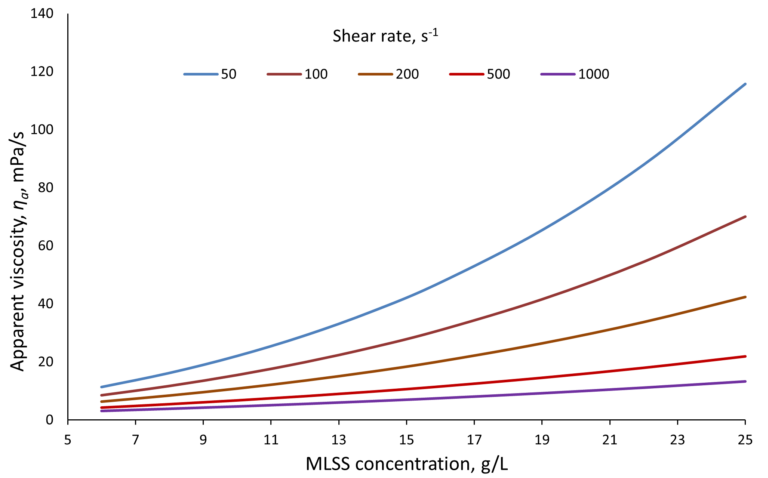
where a−d are empirical constants which have been defined by various workers (Table 1). Equation 1 therefore defines the apparent viscosity ηa for an applied shear rate γ at a given MLSS concentration X (Fig. 1).
| Reference | a | b | c | d |
|---|---|---|---|---|
| Delgado et al, 2008 | 1.71 | 0.45 | -0.068 | 0.81 |
| Laera et al, 2007 | 0.882 | 0.494 | -0.05 | 0.631 |
| Pollice et al, 2007 | 1.94 | 0.262 | -0.124 | 0.359 |
| Rosenberger et al, 2002 | 1.9 | 0.43 | -0.22 | 0.37 |
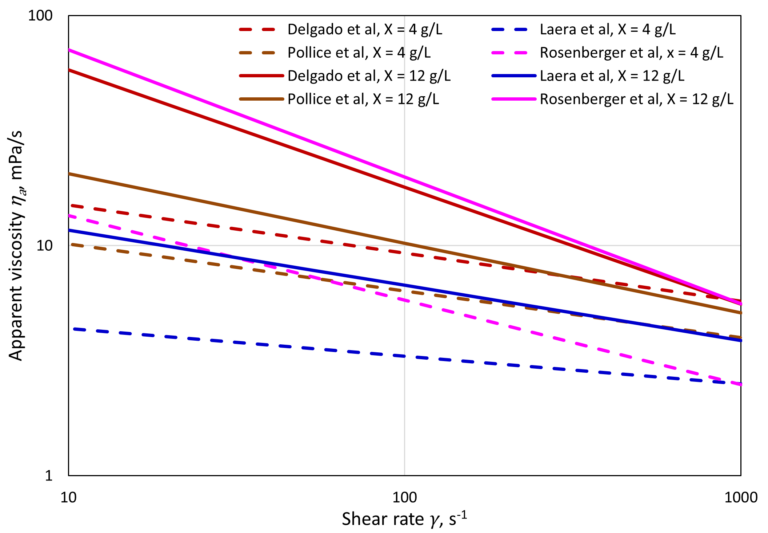
The extent to which apparent viscosity ηa
changes with shear rate γ is dependent both on the equation selected and the MLSS concentration (Fig. 2). The Rosenberger et al expression, for example, implies the strongest influence of γ
on ηa, particularly at high MLSS concentrations (Fig. 3).
The shear rate in turn depends on the liquid flow rate or, for an immersed MBR, the air scour rate. The air scour rate is defined by the specific aeration demand SADm in Nm3/h air flow per m2 membrane scoured. The shear rate applicable to an immersed flat sheet (iFS) module is generally in the range 200−1000 s-1 at the air scour rates normally employed for this configuration.